【网络流24题】魔术球问题

发表于 | 更新于 | 分类于 | 阅读次数：

蒟蒻做的第一道网络流构造题，太经典了故写题解已记之。

大多数题解都是直接从网络流角度来考虑，我觉得这样并不合适，如果比赛的时候没有TAG给你点，像这种类型的问题都很容易往找规律上靠（但此题确实可以找规律）。

于是我们引入一个叫“隐式图”的概念。

隐式图顾名思义，大白话来讲就是题目看着不像是图论，但是可以通过一些限制或关联进行建点，连边，最终通过图论的一些算法来求解。

那么就此题来看，经思考一会可发现这题的柱子并没有什么实际的作用，所有的操作都是关于珠子的编号的。那么我们可以以每一个珠子为点，若满足条件（编号相加为平方数）就两两连边，那么就可得到这样一张图：

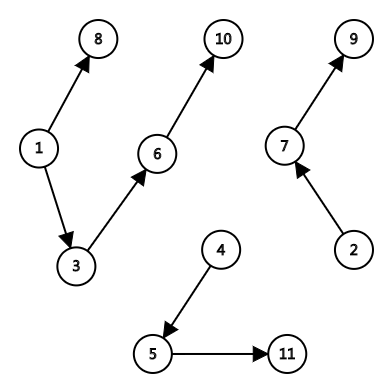
具体怎么连放代码里说。

题目要你求 “对于给定的n，计算在n根柱子上最多能放多少个球”，转化成图的问题就是 “对于给定的n，计算不超过n条路径最多可以覆盖多少满足条件的节点”，如果您已经学了$DAG$的一些二分图相关性质，应该就知道了： 

最小边覆盖=点总数-最大匹配。

有这么个性质，于是再将此图进行拆点，转化成二分图的形式，每加一个点就在上面跑匈牙利/网络流并统计总匹配，如果发现 点总数-最大匹配>最小边覆盖 那就退出。

但是值得注意的是， 我们每次重新跑网络流时，都是在跑残量网络，意思就是我们每次所得的最大流都是增加的匹配数，所以就再搞个变量累加得到总的匹配数。

但是另一个子问题是求他的路径。

其实把网络流原理搞懂了也不难，二分图里的网络流路径等价于他把流量跑满的路径（流量均为1），于是最后对每个点都找一遍，看到哪个点满流他的下一步就是那个点，储存一下最后输出即可。

上我丑陋的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
#include <iostream>
#include <algorithm>
#include <queue>
#define N 10000  //不好确定N的点数，于是加个大的。
#define NN 30000  
#define inf 2147483647
using namespace std;

struct ed{
	int u,next,w;
}e[200000];
int spr[10000],n,st=1,sum,c[50001],fir[50001],d[50100];
queue<int> q; bool v[50000];
int to[10000],pd[10000]; 

void add(int x,int y,int w)
{
	e[++st].u=y; e[st].next=fir[x]; e[fir[x]=st].w=w;
}

bool bfs()
{
	for (int i=0;i<=50000;i++) d[i]=inf/2,v[i]=0,c[i]=fir[i];
	q.push(0); v[0]=1; d[0]=0;
	while (!q.empty())
	{
		int k=q.front(); q.pop();
		for (int i=fir[k];i;i=e[i].next)
		{
			int u=e[i].u,w=e[i].w;
			if (d[u]>d[k]+1&&w)
			{
				d[u]=d[k]+1; if (!v[u]) v[u]=1,q.push(u);
			}
		}
	}
	return (d[NN]<inf/2);
}
int dfs(int p,int now)
{
	if (p==NN) return now;
	int mw=0,used=0;
	for (int i=c[p];i;i=e[i].next){
		c[p]=i; int u=e[i].u,w=e[i].w;
		if (d[u]==d[p]+1&&w)
		if (mw=dfs(u,min(w,now-used)))
		{
			e[i].w-=mw; e[i^1].w+=mw; used+=mw;
			
			if (used==now) break;
		}
	}
	return used;
}

int dinic()
{
	int ans=0;
	while (bfs()) ans+=dfs(0,inf);
	return ans;
}


int main()
{
	cin>>n;
	for (int i=1;i<=5000;i++) spr[i]=i*i;   //预处理平方数
	int num=1;
	while ("lyc qwq!")  //膜同学保平安
	{
		int kk=lower_bound(spr+1,spr+1000,num)-spr;
		//我们可以通过二分来确立当前的数最大可以匹配到那个平方数（每次都只连比他小的边，就避免了重复）	add(0,num,1),add(num,0,0),add(num+N,NN,1),add(NN,num+N,0);
        //把隐式图直接转为二分图
		for (int j=2*kk;j>=1;j--)
		{
			int k=spr[j]-num;
			if (k<num&&k>0) add(k,N+num,1),add(N+num,k,0);
			
		}
		int ans=dinic(); sum+=ans;
		if (num-sum>n) break;
        //就是那个公式的体现
		num++;	
	}
	cout<<num-1<<endl;
	for (int k=1;k<num;k++)
	{
		for (int i=fir[k];i;i=e[i].next) if (!e[i].w) {
				to[k]=e[i].u-N; break;
                //由于存二分图的时候拆点多加了N，这里减掉
			}
	}
	for (int i=1;i<num;i++)
	{
		if (pd[i]) continue; 
		for(int k=i;k>0;k=to[k])
        //递推求解。
		{
			pd[k]=1;
			cout<<k<<" ";
		}
		cout<<endl;
	}
	return 0;
}