动态规划水集(2)——基础DP：从入门到出门

$0.$前言

作为半个身子埋在物竞里面的人，暑假可能就没多少功夫管OI了。。其实如果想在物竞上有所作为的话，我现在应该直接把电脑往地上一摔，从此与OI不再往来才好。。

但出于道义也好，处于情义也罢，还是想把这玩意给好好写完。。

本文将把NOIP会考的DP模型全部说一遍，让各位有一个相对完整的技能树。至于一些优化部分可能会另开一文细谈。

$1.$线性$DP$

我们入门学的几乎全是线性DP，比较常见的有：

$LIS,LCS$问题
背包问题

目前只想到这两个比较重要的，别看模型十分简单，却可以出很难的题。

线性DP常用刷表法解决。 基本上确定DP可转移的状态，找到与已知状态间的关系，写出转移方程，之后就是很简单的事了。

$NOIP$对于线性DP的考察也很多，这里以传纸条为例。
题面：

给你一个矩阵，找两条连接对角线定点的不重合路径，使权值最大。

口胡分析：

首先看到一来一回两条路径肯定要当做两条由上及下的不重叠路径做，才符合线性DP的规则。

设$f[i][j][x][y]$为一号路径到$(i,j)$和二号路径到$(x,y)$的最大和。

那么对于两条路径，均有两种转移方案：

从上方下来，以一号路径即：$f[i][j]=f[i-1][j]+w[i][j]$
从左方过来，以一号路径即：$f[i][j]=f[i][j-1]+w[i][j]$

考虑上二号路径同理，即得线性DP转移方程：
$f[i][j][k][q]=max($

$f[i-1][j][k-1][q],f[i][j-1][k-1][q],$

一号由1，二号由1； 一号由2，二号由1

$f[i-1][j][k][q-1],f[i][j-1][k][q-1])$

一号由1，二号由2； 一号由2，二号由2

$+a[i][j]+a[k][q]$

两种路径新添价值。

最后注意路径不可重叠，特判一下，这个原因也导致$f[n][m][n][m]$无结果，取$f[n][m][n][m-1]$即可。（一道SB题说了很多。。）

$2.$树形$DP$

用来维护父亲节点与各个儿子间的关系，基本上采用$dfs$进行深搜转移。
通过这种方式，才能得到所有儿子的信息从而转移回根节点。

通常这样写：

void dfs(int u,int fa)
{
	..balala...  //处理叶子节点
	for (int i=fir[u];i;i=e[i].nex)
	{
		int v=e[i].u; if (v==fa) continue;
		dfs(v,u); 
		..balabala...  //通过子树推导当前根节点信息。
	}
	
}

比较典型的要数没有上司的舞会，这也是$2018NOIP~D2T3$的部分分，那么煞笔我居然没拿到。。

可以以最近做的有线电视网为例。

题面： 太长不复制了。。

口胡分析：

都说这题是背包，但非叶子节点价值是负数也能算背包吗（好像真的可以。。），于是就当树形DP讲了。。

虽然要求算最多可获益的人数，但这玩意明显应该作为容量来考虑。所以我们设$f[i][j]$为以$i$为根，最多可获益$j$人的最大收益（可为负）。然后找最大的$i$使收益$f[n][i]>0$即可。。

那么对于初始化，明显$f[\forall u][0]=0,f[\forall u][i]=-INF$
对于叶子结点u，$f[u][1]=a[u]$
对于非叶子节点，枚举其所有儿子$v$，则有：

$$f[u][i]=max(f[v][k]+f[u][j-k]-e[i].w)$$

即是在该儿子子树内选k个人加上除了其他儿子选(j-k)个人，最终加上价值（负的），取最大即可。

$3.$区间$DP$

区间DP通常是设$f[i][j]$表示在$[i,j]$间的某些信息，并通过拓宽边界的方式得到$[1,n]$区间的答案。

由于动态规划的无后效性，我们当然要从子结构往大的转移。对于树形DP显然就是从子树转移到根，而对于区间DP就是从小区间转移到大区间

通常这样写：

for (int l=2;l<=n;l++) //枚举长度 
for (int i=1;i<=2*n-l+1;i++)  //枚举起点
{
	int j=i+l-1; //确定终点
	for(int k=i;k<j;k++){ //寻找断点 
		...balabala...
	} 
}

比较典型的有：

NOI的傻子合并，
NOIP的不需要枚举断点~~就十分简单还装作二维区间~~的矩阵取数问题

由于不需要断点导致记忆化搜索更简单一点。。

NOIP十分经典的能量项链。

可以口胡一下题解：对于一个区间$[i,j]$枚举其断点，分析样例就可看出增加的价值即为$v[i]*v[k]* v[j]$，直接套板子子即可。

在李煜东书里面有道【IOI】多边形挺好的。

题意： 给你个环由数点和运算符边构成，要求你断一条边然后求其最值的最值。

口胡分析：
由于DP经验为0，我一开始真没想到用区间DP搞，现在想想这不和能量项链一个套路吗。。

设$f[i][j]$为$[i,j]$区间的最大计算数，很显然我们可以预处理$f[i][i]$和$f[i][i+1]$，对于$\forall f[i][j]=max(f[i][k]~op~f[k+1][j])$
，其中op为运算符，这是大概的思路。

我们敲完才发现有80分。。但这20分决定这道题是绿的还是紫的。。

经思考我们恍然大悟： 这TM负负得正啊！如果两个负数相乘要想得到最大值要求两个负数越小越好啊！

于是我们还要维护$g[i][j]$表示区间的最小计算数然后特判乘法情况：

$f[i][j]=max(g[i][k]*g[k+1][j])$
//这是负负得正的情况
$g[i][j]=min(g[i][k]*f[k+1][j],f[i][k]*g[k+1][j])$
//这是正负得负的情况

然后直接上就行了，破环为链在划水集（三）中提到就不赘述。

还有一道二维区间的棋盘分割也很考验对区间DP的理解。

题意： 给定一个棋盘，要求重复n下操作：选一个矩阵，然后把这个矩阵按水平或竖直线一分为二。这样就得到了n个独立的矩阵，求这些矩阵的平方和最大值。

口胡分析： 我们大可不用想复杂，继续套区间DP的板子。

— —先枚举小区间的边长$(l_x,l_y)$，再枚举起点$(x,y)$，最终在当前子区间内讨论DP转移就行了，这是一个区间DP的通用思路。

那我们设$f[i][j][a][b][k]$为从$(i,j)$到$(a,b)$区间内分成$k$份所得到最大分数平方。经思考可得到一下方程：

对于$k=1$的情况，很显然只要套一个二维前缀和就搞定了。
对于$k>1$的情况，我们考虑一个二维断点$(x,y)$表示此处横或竖直切一刀。

$RT:$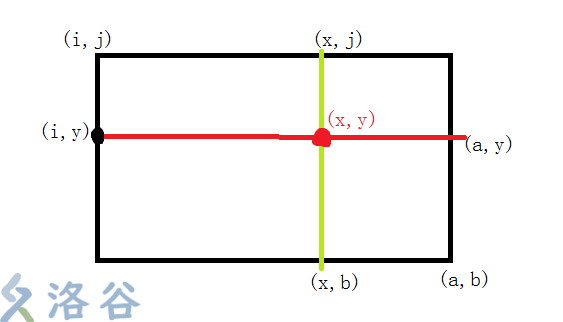

那么对于切下来的两个矩形，一个我们可以继续切而另一个要丢掉，那么就可以口胡出转移方程：

对于横着切：
$f[i][j][a][b][k]= max\begin{Bmatrix} f[i][j][a][y][1]+f[i+1][y][a][b][k-1],f[i][j][a][y][k-1]+f[i+1][y][a][b][1]\end{Bmatrix}$
↑这是分别考虑继续切下面的矩形还是切上面的矩形
对于竖着切：
$f[i][j][a][b][k]= max\begin{Bmatrix} f[i][j][x][b][1]+f[x+1][j][a][b][k-1], f[i][j][x][b][k-1]+f[x+1][j][a][b][1]\end{Bmatrix}$
↑这是分别考虑继续切右面的矩形还是切左面的矩形

然后答案就是$f[1][1][8][8][n]$，看起来十分复杂但是思路很直。

$4.$状压$DP$

状压DP虽然相比之前较难，但NOIP是考过的！啊？你问我哪题考过？

2017年的宝藏啊！虽然暴力踩标算但他好歹是标算啊！

我们这里先给出状压DP的定义：对于某集合$S$可以由其子集合$S_I$转移而来，即为状压DP。

由于状压DP中维护的状态是集合，其元素的表示我们要想做到快捷而方便的转移，最好用二进制表示。如对于一排4盏灯分别为开开关开，用二进制表示即为$(1101)_ 2$，写在$f[S]$中即为$S=13$。

由于二进制大小的限制，当$n=23$的时候就已经百万了，这导致状压DP的数据范围都很小。~~这表明当你看到一题数据范围很小而且爆搜不可做时候就上状压准没错。~~

前置芝士：位运算

首先你要知道二进制的状态集合都是通过位运算来建立关系的，就是说只有学了位运算你才能学状压。

其次你应该知道位运算的时间复杂度是$O(1)$的，也就是说只有熟练运用位运算，你才能使你的程序跑的飞快，这个在其他算法的程序也常常使用。

具体的有啥种类的位运算看下随便在网上找的博客
就行了，主要是给出一些常用手段，大家可以结合定义摸索：

判断状态$A$和状态$B$是否有重合1的部分： ~(a^b)==0
判断状态$A_i$和状态$B_j$在是否共为1： a&(1<<i) && b&(1<<j)
判断状态$A$是否有相邻1：a&(a>>1) || a&(a<<1)
判断状态$A$是否满足全集$S$: a&s==a
判断状态$A$中1的个数：
while (x) { sum++; x=x&(x-1); }

以上东西随着做题深入来补充，也欢迎大家提供一些。

其次你要注意的是：
对于每一个位运算都搞一个括号括着！

因为位运算的优先级巨低，所以对于初学者把所有位运算都拿个括号是坠吼的，当然你要是搞懂了优先级就随你便了（或者你可以记一下，位运算优先级低于逻辑判断符== ， <等）。

状压$DP$部分

状压DP难就难在他维护的是一个集合（状态），不是什么结构，因此出题十分灵活，没法子像区间，树上DP那样有明确模板。如果硬是要说的话，倒是像线性DP那样可以刷刷表啥的。。

感觉好多题想讲啊，都提一下好了。篇幅问题就都不写题面了，请大家务必好好熟悉题目再看口胡分析啊！

状压入门，$K$国王问题

首先应该先确定可以被压缩的状态，但要是选了附近一圈的格子为状态就会发现很不好转移。。

那我们就沿用刷表法的思想，以每行棋子摆放情况为一个状态，一行一行的刷。设$f[i][s][k]$为刷到第i行，此时的状态为S，此时已放了K个国王所满足的总方案数，那我们只要考虑自己行是否满足条件，上一行是否满足条件即可转移。

而且如果某限制条件只与每行自身状态有关，我们就可以先预处理出所有状态的有关信息，判断时候直接调用。 这种策略对于此题，可以解决：该状态是否存在相邻丫（zr[S]），又如该状态含有多少个1丫（ge[S]）等等，这些信息你枚举也好深搜也好都是允许的。

在预处理之后就进入的DP主体部分：

初始化：对于第一行，只要满足$zr[S]!=0,f[i][s][ge[i]]=1$
转移：对于当前第$i$行的$S$，上一行是$M$，此时已用了$l$个国王。当他们的zr[s]均为否，且相邻处也满足条件时即可转移。

其中满足条件为：

1
2
3

if(state[j] & state[p]) continue;    //上下相邻不行
if(state[j] & (state[p]<<1))    continue;   //右上角
if((state[j]<<1) & state[p])    continue;   //左上角

最终转移方程即为：
$$f[i][s][k]+=f[i-1][M][l-ge[s]]$$

其中l-ge[i]表示前$i-1$所用的国王数量。

炮兵阵地，左转划水集（3）。
$BangDream$ 的合唱站队，后面就附带详细的题解yo~
【SDOI】学校食堂也很好，但题解写不动了。。

先允许我刷刷提高训练营的题，咕一阵子。。

$5^*.$冷门$DP$

这里包含一些不常考但CSP确实可以考的模型，可能会有更多补充。

有向图$DP$

由于有向图的无后效性所诞生出来的DP种类，常常伴随拓扑排序或记忆化搜索出现，在查找图上信息时很常用。

你要问我有啥例题的话我也没做过啊，而且一时半会还找不到。只不过NOIP有道原题最优贸易可以用DP很巧妙的做出来，~~但和我用SPFA硬刚一点关系没有。~~

于是往回翻啊翻，真的找到了一道不错的$DAG~DP$题：$Running ~to ~the ~Sky$

题面： 给一张有向图, 每个点都有点权,仅第一次经过该点时该点的点权有贡献，求这张图上一条任意路径的最大贡献，若有多个则选择路径覆盖点权最大的。

口胡分析： 首先题目的第一句话暗示有子环，那我们先缩个点，然后整个图就是个DAG了，再去由入度为0的点出发，用拓扑考虑DP啥的。

基本上$DAG~DP$不会有很复杂的状态，经常都是与当前节点有关的。于是我们设$f[i]$为到第i个节点所得到的最大贡献，由于当最大贡献相同时还要考虑其路径上的最大点权，所以还需维护$p[i]$表示其最大路径上的最大点权。

于是我们在缩点的时候就要也顺便维护两个信息$:s[i],mp[i]$分别表示该连通分量的总和及其最大值，可得出最终状态方程：

初始化：$f[i]=s[i],p[i]=mp[i]$
若当前最大值需要更新：
$$f[i]=f[v]+s[i],mp[i]=max(p[i],mp[v])$$
若当前最大值相同，由于是不同路径，需要用mp数组比较：
$$mp[i]=max(mp[i],mp[v])$$

大概就是这样，若$mp[i]$的转移方程看不懂可以去原题解页面自行琢磨。

有向图DP分支— —博弈$^*$

如果当前的图可描述为一个游戏，所衍生出来的 $sg$函数 也可通过某种公式进行DP转移从而找到规律。本来我也不会，想学了之后讲讲的，但好像发现这东西其实和DP扯太远了，于是就咕了。

除了洛谷日报最近的两篇（共三篇，但第一篇博弈论就是给你讲故事的）可以参考，还可以给各位丢一个讲的很详细的博客。

期望$DP$

由于数学期望的转移具有线性关系，所以和DP也沾了不少边。但期望DP也只是作为数学期望问题的手段之一，并不是唯一的解期望题的方法，这需要注意。

前置芝士：概率与期望

由于篇幅过长就搞了一个分支啦~

期望$DP$部分

可以从最简单的一道例题，NOIP的换教室来分析一下关于期望的知识。

题面：告诉你学校各个教室距离，告诉你第i时间点上课的地点和换教室后上课地点，告诉你M次换课的概率，问你期望步行？

口胡分析：

还是好好回去把题面静下心读一下吧。。

不考虑图论部分的知识，假设已经知道个教室的距离$dis[i,j]$，我们设出$f[i][j][0/1]$表示到第I时间点，换了j次课，当前换不换所得到的最小期望距离，那怎么用期望进行分析得出方程呢？

先考虑当前不换课：

若上次也不换，那就直接$f[i][j][0]=f[i-1][j][0]+dis[a_i][a_{i-1}]$
若上次换，则由定义

可知：

E(当前上课距离)=
E(上次换了课的教室与现在教室的距离)*P(换课成功)
+E(上次没换课教室与现在教室的距离）*P(换课失败)；

显然两个事件互相独立且构成总集，所以

P(换课成功)+P(换课失败)=1

若当前换课：

若上次不换课，由定义

可知：

E(当前上课距离)
=E(上次没换课的教室与现在换课教室的距离)*P(当前换课成功)
+E(上次没换课教室与现在没换课教室的距离）*P(当前换课失败)；

对于当前“上次不换课”这个事件，换课成功和失败互相独立且构成总集，所以仍有上面那个式子。

若上次换课，继续套定义

可知：

E(当前上课距离)=
E(上次没换课教室与现在没换课教室的距离)*P(两次换课失败)
+E(上次换课教室与现在换课教室的距离）*P(两次换课成功)
+E(上次没换课的教室与现在换课教室的距离)*P(上次失败当前成功)
+E(上次换课的教室与现在没换课教室的距离)*P(上次成功当前失败)

由概率线性性质：$P(AB)=P(A)* P(B)$，且满足$\sum P(A_i)=1$ 。于是几个概率都是可算的，本题就没了。

$0.$前言

$1.$线性$DP$

$NOIP$对于线性DP的考察也很多，这里以传纸条为例。

$2.$树形$DP$

可以以最近做的有线电视网为例。

$3.$区间$DP$

比较典型的有：

在李煜东书里面有道【IOI】多边形挺好的。

还有一道二维区间的棋盘分割也很考验对区间DP的理解。

$4.$状压$DP$

前置芝士：位运算

状压$DP$部分

状压入门，$K$国王问题

$BangDream$ 的合唱站队，后面就附带详细的题解yo~

【SDOI】学校食堂也很好，但题解写不动了。。

$5^*.$冷门$DP$

有向图$DP$

有向图DP分支— —博弈$^*$

期望$DP$

前置芝士：概率与期望

期望$DP$部分

先考虑当前不换课：

若当前换课：

$6^*.$数位$DP$